Kondensatoren liefern eine Phasenverzögerung zwischen Strom und Spannung. Strom führt die Spannung um 90 Grad. Diese wurden mir nur mit den Gleichungen beigebracht. Aber ich möchte eine visuelle Intuition, was in dem Kondensator passiert, der eine Phasenverzögerung verursacht.
Gleiches gilt für die Induktivität. Bitte helfen Sie mir mit Visuals.
Leider scheinen sich die meisten Pädagogen eher auf das Auswendiglernen von Gleichungen als auf Intuition und Verständnis zu konzentrieren. Die beste "intuitive" Erklärung von Kondensatoren, die ich bisher gesehen habe, stammt von William Beaty. Hier ist ein Bild von dieser Erklärung:
Beaty spricht viel darüber, wie Dinge wirklich funktionieren, und unterscheidet zwischen dem Euklidischen und dem "Griechischen" Standpunkt "das Auswendiglernen von Gleichungen; im Vergleich zum "babylonischen Standpunkt", wo Konzepte weitaus wichtiger sind als Gleichungen. Er versucht, Bilder und Analogien zu erhalten, um etwas visuell und auf Darmebene zu verstehen. ( a)
Die meisten derartigen "intuitiven" Beschreibungen elektrischer Geräte verwenden ein hydraulische Analogie.
Sowohl bei Kondensatoren als auch bei Induktivitäten kann Energie "im" Gerät gespeichert werden. Oft wechseln wir schnell zwischen dem Einpumpen von Energie in das Gerät und dem Zurückziehen der Energie das Gerät.
Wann immer wir etwas in einer Schachtel haben, das etwas speichert - Energie, Reis, Wasser, Murmeln usw. - und wann immer wir zwischen dem allmählichen Einlegen von etwas in die Schachtel und dem allmählichen Hin- und Hergehen hin und her gehen etwas aus der Schachtel nehmen - die Spitzen (maximal) der "Menge an Sachen in der Schachtel" bleiben immer hinter dem Beginn zurück, etwas in die Schachtel zu legen. Außerdem bleibt der niedrigste Punkt in den Tälern (Minimum) "Menge an Material in der Box" immer hinter dem Beginn des Herausnehmens von Material aus der Box zurück. Der Zeitpunkt, an dem wir die maximale Menge an Material in dieser Box haben, geschieht in dem Moment, in dem wir anhalten Legen Sie Material in die Box und nehmen Sie Material aus der Box.
Wir fügen einem Kondensator mehr Energie hinzu, indem wir Elektronen auf eine Seite drücken (und die gleiche Anzahl von Elektronen auf der anderen Seite herausziehen). Die Spannung ("Druck") über dem Kondensator kann verwendet werden, um zu berechnen, wie viel Energie im Kondensator gespeichert ist.
Wir fügen einem Induktor mehr Energie hinzu, indem wir eine elektromotorische Kraft über seine Anschlüsse erzwingen. Der Elektronenfluss ("Strom") durch den Induktor kann verwendet werden, um zu berechnen, wie viel Energie "im" Induktor gespeichert ist
Denken Sie auf einfache Weise:
Ein Kondensator besteht aus zwei Platten, zwischen denen im Ausgangszustand keine Spannung liegt.
Wenn eine externe Spannung angelegt wird, liegt immer noch keine Spannung zwischen den Platten an.
Der Kondensator wird aufgeladen, um das Potential der Klemmen zu erreichen. Wenn Sie dies tun, verbraucht es Strom, zunächst den Maximalwert, dann immer weniger, wenn es in den vollen Zustand aufgeladen wird.
Und hier ist das Bild, um zu helfen:
Die blaue Wellenform ist die Eingangsschrittspannung, die schwarzen und roten sind die Spannung und der Strom durch den Kondensator. Die Formeln sind die Ihnen bekannten.
Von hier an können Sie mit dem, was Curd gesagt hat, extrapolieren und dann weiter.
Nun, so etwas sollte jeder auf seine eigene intuitive Weise verstehen. Eine Möglichkeit, diese Verzögerung darzustellen, ist folgende:
Die Gleichung, die den Kondensator beschreibt: $$ {I} _ {C} = C \ cdot \ frac {d} {dt} {U} _ { c} $$ Wir haben also eine Ableitung drin. Angenommen, die Spannung unseres Kondensators ist eine Sinuswelle. Was ist die Ableitung einer Sinuswelle? Ein Kosinus. Und umgekehrt.
Nun, ich verstehe, dass Sie bereits so viel wissen. Versuchen Sie diesen optisch ansprechenden elektronischen Simulator, um ein besseres Gefühl dafür zu bekommen, was tatsächlich mit Strom und Spannung passiert. Es gibt unzählige weitere Beispiele. Sie können Ihre eigene Schaltung erstellen und Strom und Spannung auf ansprechende Weise beobachten, anstatt Diagramme zu betrachten.
Die Person, die diesen Simulator erstellt hat, verfügt auch über viele interessante Java-Anwendungen für die Physik. Sie helfen dabei, Magnetismus, Akustik und viele andere zu verstehen.
Wenn ich unten Fehler gemacht habe, hoffe ich, dass jemand, der besser informiert ist, mich korrigiert, mich abstimmt oder was auch immer. :)
Schauen Sie sich zuerst diese beiden Quellen an, um einige schöne Diagramme der Spannung und des Stroms für Kappen und Induktivitäten zu erhalten.
Kappen: http://www.tpub.com/ neets / book2 / 4b.htm
Induktoren: http://www.tpub.com/neets/book2/4.htm
Jetzt laden Sie einen Kondensator auf, indem Sie eine Spannungsquelle anlegen, in diesem Fall Ihre Sinuswelle. Nun, die Rate, die ein Kondensator auflädt, hängt direkt mit der Änderungsrate der von Ihnen angelegten Spannungsquelle zusammen (siehe Quellen unten). Wenn Sie beginnen, Ihre Sinuswelle bei T (0) anzulegen, haben Sie die maximale Änderungsrate und somit speichert der Kondensator die Ladung mit der maximalen Rate (für diese angelegte Sinuswelle sowieso). Hier laden Sie also so schnell wie möglich auf, was bedeutet, dass Strom in den Kondensator schreit. In Wahrheit fließen Elektronen in eine Platte und aus der anderen heraus, während sie ein elektrisches Feld zwischen den beiden Platten erzeugen. Es fließt also Strom, aber er fließt nicht physisch durch den Raum oder die Dialektik zwischen beiden Platten.
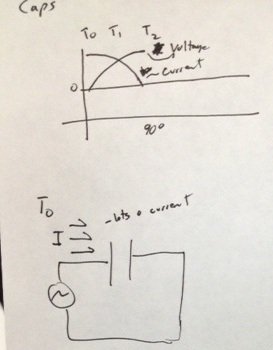
Wenn Sie nun entlang Ihrer Sinuswelle gehen, nimmt die Spannungsänderungsrate T (1) im Diagramm ab, sodass weniger Strom fließt.
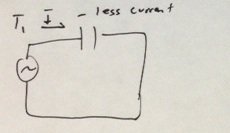
Wenn Sie zu T (2) kommen, gibt es am Nullpunkt keine Änderungsrate, sodass kein Strom fließt.
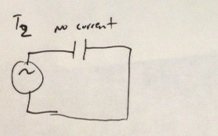
Deshalb gibt es diesen Phasendifferenz.
Nun zum Induktor. Wenn Strom in einen Induktor fließt, wird um diesen herum ein Magnetfeld erzeugt. Der Schaffung dieses Feldes steht der Raum um ihn herum gegenüber, und außerdem ändert das Material, das sich in diesem Raum befindet, das Ausmaß des Zurückdrückens, das es fühlen wird (denken Sie also an Eisenkerne usw.). Zu Beginn Ihrer Sinuswelle (T (0) im Diagramm) versuchen Sie nun, den Strom zu ändern, und der Induktor drückt auf Sie zurück und sagt, dass kein Strom fließen soll. Die Spannung versucht, Strom durchzudrücken, wodurch unser Magnetfeld erzeugt wird, das durch den Raum um sie herum zurückgedrückt wird, so dass letztendlich der Stromfluss aufgehalten wird. Grundsätzlich drückt der Induktor mit einem Spannungsabfall zurück, der den Elektronenfluss stoppt.
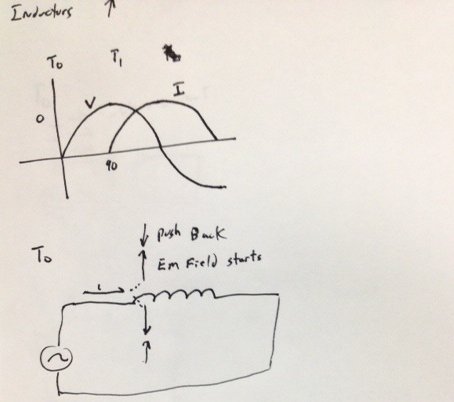
Genau dann, wenn die Spannung im zweiten Viertel eines Zyklus des Feldes abfällt Sie haben gerade angefangen zu kollabieren und Strom fließt aus der Induktivität (T (1) im Diagramm). Die Menge des Stromflusses steigt an, bis die Spannung die Nullmarke erreicht, hier fließt maximaler Strom. Wenn Sie fortfahren, steigt die Spannungsänderungsrate an und der Induktor beginnt, den Stromfluss zu drosseln, bis Sie wieder Ihre maximale Änderungsrate erreichen und überhaupt kein Fluss mehr vorhanden ist.
Ich hoffe, das hilft, auch ich habe diese andere Site als Referenz verwendet: http://www.allaboutcircuits.com/vol_1/chpt_15/1.html Sie hat eine schöne Erklärung von Induktoren.
Ich biete Ihnen keine visuellen Bilder, sondern eine irgendwie visuelle Beschreibung:
Wie Sie einen Widerstand als ein Gerät sehen können, das Strom in Spannung (sowie Spannung in Strom) "umwandelt", können Sie Sehen Sie einen Kondensator als ein Gerät, das Ladung in Spannung umwandelt.
Ladung ist Strom, der über die Zeit integriert wird.
Wenn also Strom durch einen Kondensator fließt, sehen Sie die Spannung nicht sofort, sondern nur nachdem sich eine Ladungsmenge angesammelt hat.
Der Strom durch einen Kondensator ist also proportional zur Änderungsrate der Spannung, dh proportional zur Steilheit der Spannungs-Zeit-Kurve.
Angesichts der Tatsache, dass Strom- und Spannungssignale Sinussignale sind, ergibt sich die Phasenverschiebung, weil
cos (wt) = sin (wt + 90 °)
und
d / dt sin (wt) = w * cos (wt)
Damit ein Kondensator seine Spannung erhöhen kann, muss er auf sehr intuitive Weise Ladung akkumulieren, sodass zunächst eine Weile Strom fließt. Daher bleibt die Spannung zeitlich hinter dem Strom zurück.
Zusätzlich steigt die Spannung an, wenn der Strom positiv ist (weil sich Ladung ansammelt), und nimmt ab (und wird schließlich negativ), wenn der Strom negativ ist. Folglich treten die Spannungsspitzen auf, wenn der Strom Null überschreitet (Vorzeichen ändert), weil er vom Inkrementieren zum Dekrementieren und umgekehrt wechselt. Dies erklärt die genaue 90-Grad-Phase.
Das Verhalten des Induktors kann auf sehr ähnliche Weise erklärt werden, wobei jedoch die Rollen vertauscht werden. Die Argumentation würde damit beginnen, dass für den Aufbau von Strom durch eine Induktivität eine Spannung für eine Weile vorhanden sein müsste, daher bleibt der Strom zeitlich hinter der Spannung zurück. Usw.
Für ein wirkliches Verständnis sollten wir die Mathematik verwerfen und die physikalischen Dinge fokussieren.
Denken Sie, dass jeder Kondensator nur eine Struktur aus einem Plattenpaar ist (mit einem dielektrischen Material zwischen den Platten, wie l: l). . Es kann nur verwendet werden, wenn es aufgeladen ist, d. H. Eine Platte ist mit + ve Ladung beladen (und die andere Platte ist mit -ve Ladung).
Während des Ladevorgangs erhält jede Platte die entsprechenden Ladungen und allmählich baut sich die Platte mit immer mehr Ladungen auf. Der Anstieg der Ladungen ist eigentlich der Anstieg der Ladungskonzentration, auch Anstieg des Potentials (Vc) genannt.
Um die Ladung allmählich zu erhöhen, muss der Ladelieferant mehr Potenzial als der Kondensator haben. Wenn der Lieferant ein konstantes Potential (Vs) hat, verringert sich allmählich die Potentialdifferenz (Vs-Vc), die sich allmählich ergibt Stromabfall. Schließlich erreicht Vc Vs und der Strom stoppt. Wenn wir die Situation analysieren, fällt der Ladestrom mit steigendem Kondensatorpotential (Vc).
Wenn der Ladelieferant eine Wechselstromquelle ist, steigt das Lieferantenpotential im ersten Quartal allmählich an und fällt im zweiten Viertel und so weiter. Während des 1. Quartals wird der Kondensator aufgeladen und erreicht allmählich die Quellenspannung. Während des 2. Quartals entlädt sich der Kondensator zum Lieferanten zurück, da dessen Potenzial geringer ist als der erstere. Dieses Phänomen wiederholt sich in jedem Halbzyklus. Das Laden wird als Referenzphänomen betrachtet. Der Ladungszufluss zum Kondensator ist die erste Aktion und der mögliche Aufbau ist das nachfolgende Ergebnis. Wir nennen das Potential (Spannung) nach dem Strom.