Frage:
Astable 555 Timing-Schaltung (0,5 Hz und 50% Tastverhältnis)
user43916
2014-06-03 05:06:36 UTC
view on stackexchange narkive permalink

Ich versuche, eine Zeitschaltung aufzubauen, um ein Signal mit einem Tastverhältnis von 0,5 Hz und 50% zu erzeugen. Mit anderen Worten: 1 Sekunde an, 1 Sekunde aus und so weiter ...

Ich habe einige Stellen durchsucht und die folgenden Anweisungen gefunden, aber das hat nicht funktioniert. http://electronicsclub.info/555timer.htm#dutycycle.

Irgendwelche Ideen?

Welche der Anweisungen dort haben Sie ausprobiert und wie genau hat es nicht funktioniert?
die Anweisung auf dem Link oben veröffentlicht.In der Mitte der Seite befindet sich ein Abschnitt über 50% Einschaltdauer und ein Schaltplan.Unter Verwendung der Formel Tm = 0,7 * R1 * C1 und Ts = 0,7 * R2 * C1 berechnete ich R1 und R2 zu ca. 65 K und die Kapazität zu 22 UF, aber ich erhalte nur 1,5 ms Zeit, was keinen Sinn ergibt, und das auchist 5% Einschaltdauer statt 50% zu schließen.
@user43916 Fügen Sie Ihre Berechnung in den Hauptteil der Frage ein und teilen Sie uns mit, was Sie haben und was Sie erwartet haben.Wenn Sie spezielle Fragen haben, stellen Sie diese.Zum späteren Nachschlagen: "Irgendwelche Ideen?"ist keine spezifische Frage.Weder "das hat nicht funktioniert" ist spezifisch.Es stellt sich heraus, dass "das" eine Berechnung war, die nicht funktioniert hat ... Wer hätte das gedacht?
@user43916 Willkommen bei EE.SE übrigens.
Hmmm ... die Site, auf die Sie sich beziehen, sagt, dass die Formel "Tm = 0,7 × (R1 + R2) × C1" ist.Das Tastverhältnis nähert sich 50%, wenn sich R1 0 nähert. Versuchen Sie R1 = 1k, R2 = 150k, C = 10uF.
Zehn antworten:
mbmast
2016-06-02 00:44:22 UTC
view on stackexchange narkive permalink

Siehe die Beschreibung von "Better Timing" in 555 Timer Circuits. Diese Schaltung eliminiert das klassische R2, fügt einen NPN-Transistor hinzu (2N3904 ist in Ordnung), ein neues R2, um nur den hinzugefügten NPN-Transistor vorzuspannen (d. H. Nicht an der RC-Schaltung teilzunehmen), und zwei Dioden, um den Kondensator über R1 zu laden und zu entladen. Dies ergibt ein Tastverhältnis von 50% (da das Laden und Entladen über denselben einzelnen Widerstand erfolgt).

Von der verknüpften Site:

[Better Timing]

Auch von der verlinkten Seite:

Durch Hinzufügen eines Transistors und einer Diode zum RC-Timing-Netzwerk wird ein besserer und stabilerer Timing-Ausgang erzeugt. Die Frequenz kann über einen weiten Bereich variiert werden, während ein konstanter Arbeitszyklus von 50% beibehalten wird. Wenn der Ausgang hoch ist, wird der Transistor durch R2 in die Sättigung vorgespannt, so dass der Ladestrom durch den Transistor und R1 nach C fließt. Wenn der Ausgang niedrig wird, schneidet der Entladungstransistor (Pin 7) den Transistor ab und entlädt den Kondensator durch R1 und die Diode. Die hohen &-Niedrigperioden sind gleich. Der Wert des Kondensators (C) und des Widerstands (R1 oder Potentiometer) wird nicht angegeben. Dies ist nur ein Beispiel dafür, und die Werte hängen vom Anwendungstyp ab. Wählen Sie daher Ihre eigenen Werte aus. Die Diode kann eine beliebige kleine Signaldiode wie die NTE519, 1N4148, 1N914 oder 1N3063 sein, aber ein Germanium- oder Schottky-Typ mit hoher Leitfähigkeit für die Diode minimiert die Diodenspannungsabfälle im Transistor und in der Diode. Der Transistor sollte jedoch ein hohes Beta aufweisen, damit R2 groß sein kann und der Transistor dennoch gesättigt wird. Der Transistor kann ein TUN (Europa), NTE123, 2N3569 und die meisten anderen sein.

EM Fields
2014-06-03 06:05:33 UTC
view on stackexchange narkive permalink

Mit der herkömmlichen stabilen Anordnung mit 2 Widerständen und 1 Kondensator ist es unmöglich, eine 50% ige Ausgabe von einem 555 zu erhalten.

Der einfachste Weg ist die Verwendung eines CMOS 555 und die Verwendung der auf der Titelseite gezeigten Schaltung von:

http://datasheets.maximintegrated.com/de/ds/ICM7555-ICM7556.pdf

Der nächst einfachere Weg und der Weg Um einen Arbeitszyklus von <1% bis> 99% zu erreichen, muss eine Diodensteuerung um die Widerstände des Astables verwendet werden.

Um die genauesten 50% zu erhalten, stellen Sie den 555 so ein, dass er die doppelte Frequenz ausgibt, die Sie möchten, und dann eine Division durch zwei an seinem Ausgang mit einem Flip-Flop vom Typ "D" durchführen.

hkBattousai
2015-06-22 16:00:57 UTC
view on stackexchange narkive permalink

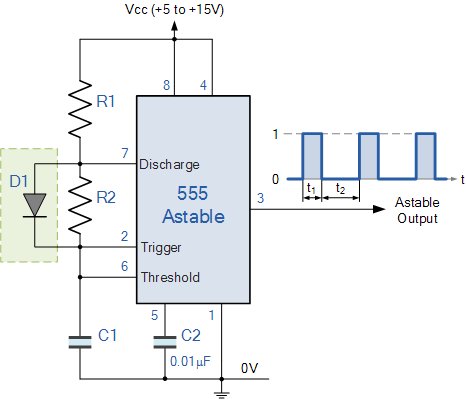
enter image description here

enter image description here

In dieser modifizierten astabilen Multivibratorschaltung wird der Durchlassspannungsabfall der Diode D1 immer ignoriert, und die Zeitformeln werden als angegeben p>

$$ t_1 = \ ln (2) R_1C_1, \ quad t_2 = \ ln (2) R_2C_1. $$

Wenn Sie \ $ R_1 = R_2 \ $ nehmen und den Spannungsabfall der Diode ignorieren, erreichen Sie ein Tastverhältnis von% 50. Was passiert jedoch, wenn wir den Spannungsabfall der Diode nicht ignorieren?

Angenommen, der Durchlassspannungsabfall von D1 beträgt \ $ V_D \ $. Die Spannung an Pin 5 ist \ $ \ dfrac {2} {3} V_ {cc} \ $.

Die allgemeinste Form der Kondensatorladegleichung ist

$$ v_c (t) = V_s + \ left [v_c (t_0) - V_s \ right] e ^ {- \ dfrac {t-t_0} {RC}}, \ quad t \ ge t_0. $$

Wenn wir die Begriffe neu anordnen, um den Zeitunterschied zu erhalten, erhalten wir

$$ \ Delta t = t - t_0 = RC \ ln \ left [\ dfrac {V_s - v_c (t_0)} {V_s - v_c (t)} \ right]. $$

Wobei \ $ v_c (t) \ $ die Funktion der Kondensatorspannung ist, \ $ V_s \ $ die Quellenspannung.

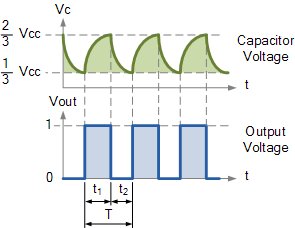
Während der Einschaltdauer ist die Der Kondensator C1 wird über R1 von \ $ \ dfrac {1} {3} V_ {cc} \ $ nach \ $ \ dfrac {2} {3} V_ {cc} \ $ aufgeladen. Die Versorgungsspannung, die dieses RC-Netzwerk sieht, ist \ $ V_ {cc} -V_D \ $.

$$ t_1 = R_1C_1 \ ln \ left [\ dfrac {V_ {cc} - V_D - \ dfrac {1 } {3} V_ {cc}} {V_ {cc} - V_D - \ dfrac {2} {3} V_ {cc}} \ right] = R_1C_1 \ ln \ left [\ dfrac {\ dfrac {2} {3 } V_ {cc} - V_D} {\ dfrac {1} {3} V_ {cc} - V_D} \ right] = R_1C_1 \ ln \ left [1 + \ dfrac {V_ {cc}} {V_ {cc} - 3V_D} \ right] $$

Während der Entladung hat D1 keine Wirkung. In ähnlicher Weise ist \ $ t_2 \ $

$$ t_2 = R_2C_1 \ ln \ left [\ dfrac {V_ {cc} - \ dfrac {1} {3} V_ {cc}} { V_ {cc} - \ dfrac {2} {3} V_ {cc}} \ right] = \ ln (2) R_2C_1. $$

Dann ist die Periode der Schwingung

$$ \ boxed {T = t_1 + t_2 = R_1C_1 \ ln \ left [1 + \ dfrac {V_ {cc}} {V_ {cc} - 3V_D} \ right] + \ ln (2) R_2C_1}. $$

Und die Häufigkeit ist

$$ \ boxed {f = \ dfrac {1} {T} = \ dfrac {1} {t_1 + t_2} = \ dfrac { 1} {R_1C_1 \ ln \ left [1 + \ dfrac {V_ {cc}} {V_ {cc} - 3V_D} \ right] + \ ln (2) R_2C_1}}. $$

(Angepasst an diese Frage.)

Kompensation des Fehlers aufgrund eines Diodenvorwärtsspannungsabfalls

Wir möchten, dass die Ein- und Ausschaltzeiten gleich sind. Das ist

$$ t_1 = t_2. $$

Dann

$$ R_1C_1 \ ln \ left [1 + \ dfrac {V_ {cc}} {V_ {cc} - 3V_D} \ right] = \ ln (2) R_2C_1, \\\ ln \ left [1 + \ dfrac {V_ {cc}} {V_ {cc} - 3V_D} \ right] = \ dfrac {R_2} {R_1} \ ln (2), \\ \ boxed {R_1 = R_2 \ dfrac {\ ln (2)} {\ ln \ left [1 + \ dfrac {V_ {cc}} {V_ {cc} - 3V_D} \ right]} \ quad \ quad \ text { oder} \ quad \ quadR_2 = R_1 \ dfrac {\ ln \ left [1 + \ dfrac {V_ {cc}} {V_ {cc} - 3V_D} \ right]} {\ ln (2)}}. $$

Sie müssen \ $ R_1 \ $ und \ $ R_2 \ $ proportional zueinander auswählen, um ein genau symmetrisches Tastverhältnis von 50% zu erreichen.

Warum ist ein Arbeitszyklus von 50% nicht möglich?Sie können immer R2
Olin Lathrop
2016-06-02 01:36:10 UTC
view on stackexchange narkive permalink

Tun Sie dies mit einem billigen und kleinen Mikrocontroller wie dem PIC 10F200. Das erfordert nur zwei Teile, das Mikro, das in einem SOT-23-Paket erhältlich ist, und die Bypass-Kappe.

Dann holen Sie sich einen 666 s> 555-Timer von Ihrem Lieblingsgeschenkladen im Museum und kleben Sie es über den PIC und die Kappe, um der Welt zu zeigen, dass es mit einem 555-Timer gemacht wird. Diejenigen, die nicht zu genau hinschauen, werden sich am Kopf kratzen, weil Sie die Genauigkeit so hoch und die Drift und den Stromverbrauch so niedrig erhalten haben.

Fügen Sie für zusätzliche Gutschrift ein paar weitere Teile hinzu, um sie wirklich herzustellen kratzen sich am Kopf. Der Museumsgeschenkladen wird sicherlich auch 741 Opamps haben. Holen Sie sich die in einer Dose für den besten nostalgischen Look.

WhatRoughBeast
2014-06-03 23:22:25 UTC
view on stackexchange narkive permalink

Ihre Berechnungen sind falsch, aber nicht so falsch. Die Verwendung gleicher 65k-Widerstände sollte ein Tastverhältnis von 33% ergeben (t1 = 0,7 R1 C, t2 = 0,7 (R1 + R2) C). Ihre Berechnungen wurden korrekt durchgeführt, da Ihre Formeln falsch waren und die von Ihnen verwendeten Werte einen Gesamtzeitraum von 3 Sekunden anstelle von zwei Sekunden ergeben sollten. Die Änderung des Arbeitszyklus deutet darauf hin, dass entweder einer Ihrer Widerstandswerte falsch ist (und Sie ihn messen müssen) oder Sie den Chip falsch verdrahtet haben. Ihr Gesamtzeitpunkt deutet darauf hin, dass Ihr Kondensator weit entfernt ist. Ich schlage vor, dass Sie einen 22 nF-Kondensator anstelle eines 22 uF verwenden.

tcrosley
2014-11-10 07:17:55 UTC
view on stackexchange narkive permalink

Mit diesem Rechner konnte ich die folgenden Werte berechnen: 

  R1 = 1KR2 = 360KC1 = 4 µFFrequenz = 0,5 HzPeriode = 1,999s50,07% Arbeitszyklus1.001s ein, 997.2 ms aus

, was ziemlich genau richtig ist. 360K ist jedoch nicht der Standardwiderstandswert. der nächste ist 357K. Dies ergibt: 

  R1 = 1KR2 = 357KC1 = 4 µFFrequenz = 0,505 HzPeriode = 1,982s50,07% Einschaltdauer992,37 ms ein, 989,6 ms aus

Die Sorge um den durch das 3K verursachten Unterschied ist jedoch ziemlich irrelevant, da Sie die Toleranz der Komponenten berücksichtigen müssen. Angenommen, Sie verwenden 1% -Widerstände, hat eine Änderung des Werts von R1 um 1% nur geringe Auswirkungen, und eine Änderung des Werts von R2 um 1% betrifft etwa die oben gezeigte Änderung von 350 KB auf 357 KB.

Das Problem ist der Kondensator C1. Viele Kondensatoren haben eine Toleranz von ± 20%. Dies bedeutet, dass die 4-µF-Kappe von 3,2 µF bis 4,8 µF variieren kann, wodurch die Periode von 1,586 s bis 2,378 s variiert. Glücklicherweise kann dies durch Ändern von R2 kompensiert werden; 3,2 µF zusammen mit R2 = 450 K werden auf das oben gezeigte ursprüngliche Timing zurückgesetzt, ebenso wie 4,8 µF zusammen mit R2 = 300 K. Unterm Strich müssen Sie also, sobald Sie einen Kondensator ausgewählt haben, R2 anpassen, um die benötigte Periode zu erhalten.

Ich schlage vor, zunächst einen 500K-Poti für R2 zu verwenden erforderliche Zeit, dann messen Sie die Einstellung des Topfes und ersetzen Sie ihn durch einen festen Widerstand.

Lore
2015-06-22 15:16:17 UTC
view on stackexchange narkive permalink

Folgen Sie diesem Bild:

555 astable

Wählen Sie R1 = R2 und schalten Sie eine Diode parallel zu R2, wobei die Kathode dem Kondensator C zugewandt ist.

T1 ist = 0,693 × R1 × C

T2 ist = 0,693 × R2 x C

Volt333
2017-06-01 17:23:53 UTC
view on stackexchange narkive permalink

enter image description here

Halten Sie die Lade- und Entladezeit des Kondensators gleich.Etwa 0,49 - 0,5 Hz bei 50% Einschaltdauer.

Markus
2020-03-10 18:13:01 UTC
view on stackexchange narkive permalink

Bevor Sie komplexere Dinge entwerfen, werfen Sie bitte einen Blick auf Seite 16 http://www.ti.com/lit/ds/symlink/lmc555.pdf enter image description here

Joe Tries Hard
2014-11-10 02:49:09 UTC
view on stackexchange narkive permalink

Ich habe die fragliche Schaltung in diesem Thread mit dem 555 im Astable-Modus erstellt, der die Verwendung einer 1uf-Kappe für C1 beinhaltete. R1 war 100k, R2 war 1Meg, keine Kappe an Pin 5 (Steuerspannung), keine Diode über R2 wie vorgeschlagen, um das Tastverhältnis zu senken. Das Ergebnis war eine 53% ige Einschaltdauer bei 0,5 Hz (oder sehr nahe daran). Die Versorgungsspannung betrug 12 VDC, aber es gab ein 8-Volt-Überschwingen beim Anstieg mit einer Dauer von 12 Mikrosekunden. Daher fügte ich eine 0,01uf-Keramikscheibenkappe über Ausgangspin 3 und Masse hinzu. Sie erzeugte oben eine sehr leichte Ladungskurve, beseitigte jedoch die Spitze wurde erwartet. Ich habe dies verwendet, um eine andere Schaltung zu steuern, die ich gebaut habe und die einen anderen 555 und einen Operationsverstärker LM339 (oder LM393) verwendet. Es wird ein 1-Megapot-Topf verwendet, der an Pin 2 & 6 angeschlossen ist (zwischen - und + an der Versorgungsspannung, wobei der Scheibenwischer an Pin 2 & 6 am zweiten 555 angeschlossen ist), um die Frequenz am zweiten 555 (Ausgang) einstellen zu können Die Pins 3 (& 5) wurden im zweiten Stromkreis nicht verwendet. Dann habe ich einen 50k-Poti am negativen Eingang des Operationsverstärkers verwendet, um das Tastverhältnis einzustellen. Der Wischer dieses Topfes ist mit der negativen Seite des Operationsverstärkers verbunden. Der positive Eingang des Operationsverstärkers kam von Pin 7 am zweiten 555.Hinweis: Sie können den Wert von R2 erhöhen oder den Wert von R1 senken, um das Tastverhältnis zu erhöhen (bei dem ersten 555, der in diesem Thread behandelt wird).

Das Endergebnis für den endgültigen Ausgang war "fast eine halbe Sekunde lang ausgeschaltet" und oszillierte dann mit 4 Hz, während "ein" oder "hoch". Ich habe nur einen Ausgang des Operationsverstärkers verwendet Ein NMOS für den Ausgang des Operationsverstärkers muss eingeschaltet sein, während der Ausgang hoch war, und dann ein PMOS für einen "Ein" -Ausgang im niedrigen Zustand verwenden. Dies erzeugt einen Wechselausgang von nur einem Operationsverstärkerausgang für ungefähr 1/2 Sekunde (basierend auf der Frequenz und dem Arbeitszyklus des ersten 555), dann für ungefähr eine halbe Sekunde aus. Ich kann den Arbeitszyklus und die Frequenz nach Belieben einstellen, aber der erste 555 ist auf einen Arbeitszyklus von 53% bei festgelegt. 5 Hz Die zweite Schaltung mit dem zweiten 555 und einem Operationsverstärker wird 188 kHz erzeugen. Ich war ziemlich überrascht, dass es so hoch gehen würde, ich hatte bestenfalls 125 kHz erwartet. Die Wellenformen sind eher spitz als alles, was einer Rechteckwelle ähnelt, aber es funktioniert. Alles, was höher als 188 kHz war, war zu viel, der 555 würde nicht schneller fahren. Die MOSFETS und der Operationsverstärker konnten damit umgehen, aber nicht der von mir verwendete 555 (NE555N). Zumindest war dies meine Schlussfolgerung, die auf dem Prozess der Eliminierung und weiteren Tests mit verschiedenen Widerständen und Kappen beruhte. Ich verwende die zweite Schaltung als Treiber mit variabler Frequenz und variablem Arbeitszyklus, um neue Designs für andere Schaltungen zu testen. Es verwendet eine 470nf-Kappe für das volle Potential am oberen Ende der Frequenz und eine 47nf-Kappe für das untere Ende. Es wird ein Tastverhältnis von 0,3 bis 99% und von 0,3 Hz bis 188 kHz eingestellt.
Ich hoffe, dies hilft jemand anderem. Ich kann den Schaltplan an jeden senden, der ihn möchte, oder ich kann bei Interesse einen Link dazu posten. Schlussbemerkung: Diese kombinierte Schaltung verbraucht nur 56 mA bei einer Last von 36 mA (Durchschnitt 56 mAh). Ich habe einen Datenlogger über einen Zeitraum von 10 Minuten in Intervallen von 1 Sekunde für die Abtastrate verwendet und ihn dann zur Analyse in eine EXCEL-Tabelle heruntergeladen.

Ich habe vor zwanzig Jahren Schaltkreise entworfen, aber die Dinge haben sich sehr geändert seitdem muss ich also viele neue Geräte von Grund auf neu lernen. Wenn ich bei der Erklärung Fehler gemacht habe, können Sie mich gerne darauf hinweisen !! :-)

Danke !!!

Joe

Bitte posten Sie einen Link zum Schaltplan oder bearbeiten Sie Ihre Antwort, noch besser, damit sie den Schaltplan selbst enthält.


ⓘ
Diese Fragen und Antworten wurden automatisch aus der englischen Sprache übersetzt.Der ursprüngliche Inhalt ist auf stackexchange verfügbar. Wir danken ihm für die cc by-sa 3.0-Lizenz, unter der er vertrieben wird.
Loading...