Beispielschema
Finden Sie zu Ihrer Unterhaltung eine Analyse der folgenden Schaltung:
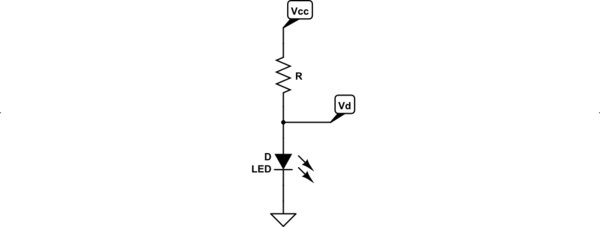
simulieren diese Schaltung - Schema erstellt mit CircuitLab sup>
(Der größte Teil des hier folgenden Materials ist auf dieser Wikipedia-Site leicht zu finden: Diodenmodellierung. Ich werde jedoch einen anderen Ansatz für die Antwort auf die geschlossene Lösung wählen.)
Shockley-Diodengleichung
Unter der Annahme, dass der Betrieb bei seiner Kalibrierungstemperatur erfolgt, ist die einzige relevante Gleichung für die LED die Shockley-Diodengleichung:
$$ I_ \ text {D} = I_ \ text {SAT} \ left (e ^ {\ frac {V_ \ text {D}} {\ eta \, V_T }} - 1 \ right) $$ span>
Diese Gleichung wird leicht überarbeitet, um nach \ $ V_ \ text {D} \ $ span>:
zu lösen
$$ V_ \ text {D} = \ eta \, V_T \, \ operatorname {ln} \ left (\ frac {I_ \ text {D}} {I_ \ text {SAT}} + 1 \ right) $$ span>
Wir haben also zwei verschiedene Perspektiven auf die Diode / LED.
Bei einem diodenverbundenen Kleinsignal-BJT ist der Emissionskoeffizient (auch bekannt als Nichtidealitätsfaktor ) normalerweise \ $ \ eta = 1 \ $ span>. Für viele diskrete Dioden wie 1N4148 oder 1N4007 gilt jedoch \ $ \ eta>1 \ $ span>. (Es wird nicht kleiner als 1 sein.) Einige LEDs haben ziemlich hohe Werte (über 4, nicht selten).
Der Sättigungsstrom \ $ I_ \ text {SAT} \ $ span> wird am besten als extrapolierter \ $ angesehen y \ $ span> -Achsenabschnitt. Ich spreche darüber hier und auch hier und hier.
\ $ V_T = \ frac {k \, T} {q} \ $ span> ist die statistische thermische Spannung und ein grundlegender physikalischer Parameter mit vielen wichtigen Verwendungen. Bei Raumtemperatur wird häufig angenommen, dass es sich um \ $ \ ca. 26 \: \ text {mV} \ $ span> handelt.
Mathematische geschlossene Lösung
Die KVL-Gleichung für die obige Schaltung lautet:
$$ \ begin {align *}
V_ \ text {CC} - R \, I_ \ text {D} - V_ \ text {D} & = 0 \: \ text {V} \\\\
V_ \ text {CC} - R \, I_ \ text {D} - \ eta \; V_T \, \ ln {\ left (\ frac {I_ \ text {D}} {I_ \ text {SAT}} \ right )} & = 0 \: \ text {V}
\ end {align *} $$ span>
Das Problem hierbei ist die Lösung für \ $ I_ \ text {D} \ $ span>. Sie können dies leicht iterativ lösen. Wenn Sie ein Stück Papier mit der aufgezeichneten Diodengleichung haben, können Sie mit einem Lineal die "Lastlinie" des Widerstands hinzufügen und einen ungefähren Achsenabschnitt finden. Für eine geschlossene mathematische Lösung ohne Iteration benötigen Sie jedoch die Produktprotokollfunktion (auch bekannt als LambertW-Funktion):
$$ \ begin {align *}
V_ \ text {CC} - R \, I_ \ text {D} - \ eta \; V_T \, \ ln {\ left (\ frac {I_ \ text {D}} {I_ \ text {SAT}} \ right )} & = 0 \: \ text {V} \\\\
\ frac {V_ \ text {CC}} {\ eta \, V_T} - \ frac {R \, I_ \ text {D}} {\ eta \, V_T} & = \ ln {\ left (\ frac {I_ \ text {D}} {I_ \ text {SAT}} \ right)} \\\\
e ^ {^ {\ frac {V_ \ text {CC}} {\ eta \, V_T} - \ frac {R \, I_ \ text {D}} {\ eta \; V_T}}} & = \ frac { I_ \ text {D}} {I_ \ text {SAT}} \\\\
1 & = \ frac {I_ \ text {D}} {I_ \ text {SAT}} \ cdot e ^ {^ {\ frac {R \, I_ \ text {D}} {\ eta \, V_T} - \ frac {V_ \ text {CC}} {\ eta \, V_T}}} \\\\
e ^ {^ {\ frac {V_ \ text {CC}} {\ eta \, V_T}}} & = \ frac {I_ \ text {D}} {I_ \ text {SAT}} \ cdot e ^ {^ {\ frac {R \, I_ \ text {D}} {\ eta \, V_T}}} \\\\
\ frac {R \, I_ \ text {SAT}} {\ eta \, V_T} \ cdot e ^ {^ {\ frac {V_ \ text {CC}} {\ eta \, V_T}}} & = \ frac {R \, I_ \ text {D}} {\ eta \, V_T} \ cdot e ^ {^ {\ frac {R \, I_ \ text {D}} {\ eta \, V_T}}} \\\ \.
& \ text {set} u = \ frac {R \, I_ \ text {D}} {\ eta \, V_T} \\\\ & \ also \\\\
u \, e ^ u& = \ frac {R \, I_ \ text {SAT}} {\ eta \, V_T} \ cdot e ^ {^ {\ frac {V_ \ text {CC}} {\ eta \, V_T }}} \\\\
u& = \ operatorname {LambertW} \ left (\ frac {R \, I_ \ text {SAT}} {\ eta \, V_T} \ cdot e ^ {^ {\ frac {V_ \ text {CC}} {\ eta \, V_T}}} \ right) \\\\
\ frac {R \, I_ \ text {D}} {\ eta \, V_T} & = \ operatorname {LambertW} \ left (\ frac {R \, I_ \ text {SAT}} {\ eta \, V_T} \ cdot e ^ {^ {\ frac {V_ \ text {CC}} {\ eta \, V_T}}} \ right) \\\\
I_ \ text {D} & = \ frac {\ eta \, V_T} {R} \ cdot \ operatorname {LambertW} \ left (\ frac {R \, I_ \ text {SAT}} {\ eta \, V_T} \ cdot e ^ {^ {\ frac {V_ \ text {CC}} {\ eta \, V_T}}} \ right)
\ end {align *} $$ span>
(Weitere Informationen zur Produktprotokollfunktion, auch bekannt als LambertW, finden Sie auf der LambertW-Website von Wolfram.)
Nehmen wir nun an, \ $ V_ \ text {CC} = 9 \: \ text {V} \ $ span> und \ $ R = 220 \: \ Omega \ $ span>. Verwenden wir für die LED Parameter, die von einer Luminus PT-121-B-LED stammen: \ $ \ eta = 8.37 \ $ span> und \ $ I_ \ text {SAT} = 435.2 \: \ text {nA} \ $ span>. (Angenommen, \ $ V_T \ ca. 26 \: \ text {mV} \ $ span>.) Dann würden wir \ $ I_ \ text {D} \ ca. 29,9 \: \ text {mA} \ $ span> und \ $ V_ \ text {D} \ ca. 2,42 \: \ Text {V} \ $ span>. Dies kommt der Gewürzsimulation für das Gerät und die Umstände sehr nahe.
Oder nehmen wir an, wir verwenden die Parameter für 1N4148, \ $ \ eta = 1.752 \ $ span> und \ $ I_ \ text {SAT} = 2.53 \: \ text {nA} \ $ span> und verwenden Sie \ $ V_ \ text {CC} = 5 \: \ text {V} \ $ span> und \ $ R = 1 \: \ text {k} \ Omega \ $ span>. Dann würden wir für diese gemeinsame Diode \ $ I_ \ text {D} \ ca. 4,34 \: \ text {mA} \ $ span> und \ $ V_ \ text {D} \ ca. 654 \: \ text {mV} \ $ span>.
Wie Sie sehen, funktioniert dies für alle Diodentypen. (Die Hauptbeschränkung ist die Tatsache, dass \ $ I_ \ text {SAT} \ $ span> über die Temperatur stark variiert - diskutiert gegen Ende der Diskussion über ' vereinfachte Diodenmodelle, in denen ihre Variationen aufgrund eines der wichtigsten Ergebnisse der statistischen Mechanik, des Boltzmann-Faktors, weiter diskutiert werden.)
Zusammenfassung
Geschlossene Lösungen für grundlegende Diodenfragen sind niemals grundlegend. Für die meisten Zwecke reicht es jedoch normalerweise aus, einige vereinfachende Annahmen zu treffen und "in jeder Hinsicht nah genug zu sein". (Um einige davon zu lesen, lesen Sie 'vereinfachte Diodenmodelle', die bereits vorhin erwähnt wurden.) Sie werden die oben genannten Arbeiten wahrscheinlich nie wirklich ausführen müssen. Es ist einfach schön zu wissen, worum es geht, wenn Sie sich darüber wundern. (Meistens werden Sie also erkennen, warum Sie stattdessen diese vereinfachenden Annahmen verwenden.)
Beachten Sie auch, dass die geschlossene Lösung eine groß angelegte Lösung ist und die Frage über einen sehr, sehr großen Bereich von Umständen löst.
Sie haben sich gefragt, was passiert, wenn die angelegte Spannung der Diodenspannung entspricht. In der Realität passt sich die Diodenspannung jedoch den Umständen an. Es ist nicht behoben. Wenn Sie also versuchen, die sogenannte "Diodenspannung" an die Schaltung anzulegen, stellt die Diode stattdessen ihre Spannung noch niedriger ein, so dass der Spannungsabfall des Widerstands "gerade genug" ist, um den Strom zu liefern, der "gerade genug" ist ergeben die benötigte Diodenspannung, um die Differenz auszugleichen. Das ist hier die wahre Antwort. Die obige mathematische Lösung ist nur eine komplizierte Art, dasselbe zu sagen, aber quantitativ statt "handwedelnd".
Alle oben genannten Punkte gelten genau wie für jede in Vorwärtsrichtung vorgespannte Diode jeglicher Art. Sogar solche mit einem erheblichen (in der Anwendung) ohmschen Leitungswiderstand (der dann nur zur Analyse zum Serienwiderstand addiert wird).