Die Double-Dabble -Technik konvertiert Binärdaten durch wiederholtes Verschieben in BCD. Jede Wiederholung halbiert die verbleibende Binärzahl und verdoppelt die BCD-Zahl. Nachdem der vollständige Binärwert verschoben wurde, wird das Ergebnis erhalten. Nach jeder Verschiebung wird eine Korrektur auf jede 4-Bit-BCD-Spalte angewendet (oder auf solche mit mehr als 3 Bits, die um diesen Punkt verschoben wurden). Diese Korrektur sucht nach Ziffern, bei denen die Dezimalzahl 9 -> 10 bei der nächsten Schicht überläuft, und korrigiert das Ergebnis durch Hinzufügen von drei .

Warum drei? BCD-Ziffern im Bereich von null bis vier (0,1,2,4) verdoppeln sich nach der Verschiebung auf natürliche Weise auf 0,2,4,8. Wenn Sie 5 b 0101 untersuchen, wird dies zu b 1010 (0xA) verschoben, was keine BCD-Ziffer ist. 5 wird daher auf (3 + 5) korrigiert, dh b 1000 (0x8), was sich während der Verschiebung auf 16 Dezimalstellen (0x10) verdoppelt, was einen Übertrag von 1 zur nächsten Ziffer und der erwarteten Null darstellt.

Implementierungen wiederholen diesen Vorgang entweder zeitlich synchron unter Verwendung eines Schieberegisters und von 'n' Zyklen für einen n-Bit-Eingang oder im Raum, indem sie die Logikschaltungen für die Korrektur platzieren, die sich gegenseitig speisen und die Verschiebung durchführen mit Verkabelung. Es gibt einen Übertragspfad durch jede Ziffer, und die Übertragslogik ist nicht für die FPGA-Übertragungskettenlogik (binär) geeignet, sodass die Raumimplementierung im Allgemeinen inakzeptable Zeitsteuerungsergebnisse für große Eingaben liefert. Ein typischer technischer Kompromiss.

Für eine parallele (asynchrone) Konvertierung

Für enge Werte wie Ihren Dr. Auf der Website von John Loomis finden Sie eine Anleitung zur Logikstruktur, die für die Implementierung in Hardware erforderlich ist. Moderne umprogrammierbare Logik kann nach aggressiver Synthese eine Breite von 8 Bit bis zu 100 MHz erreichen. Das Modul add3 nimmt eine 4-Bit-Eingabe und gibt sie wörtlich aus, oder wenn mehr als vier, fügt es drei hinzu:

  Modul add3 (in, out); input [ 3: 0] in; Ausgabe [3: 0] out; reg [3: 0] out; immer @ (in) case (in) 4'b0000: out < = 4'b0000; // 0 -> 0 4'b0001: out < = 4'b0001;
4'b0010: out < = 4'b0010; 4'b0011: out < = 4'b0011; 4'b0100: out < = 4'b0100; // 4 -> 4 4'b0101: out < = 4'b1000; // 5 -> 8 4'b0110: out < = 4'b1001; 4'b0111: out < = 4'b1010; 4'b1000: out < = 4'b1011; 4'b1001: out < = 4'b1100; // 9 -> 12 default: out < = 4'b0000; endcaseendmodule  

Die Kombination dieser Module ergibt die Ausgabe.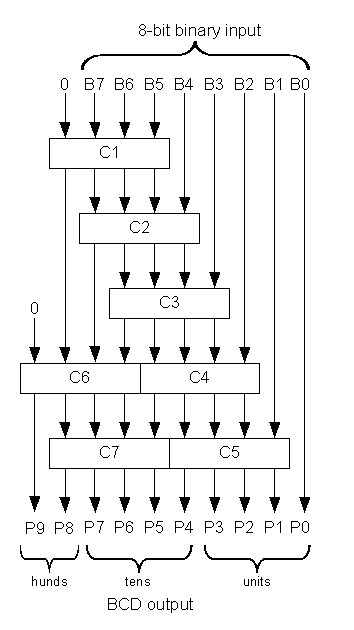

Für eine sequentielle Variante (mit mehreren Zyklen, Pipeline)

Für Wide signalisiert eine serielle Technik, die in Xlinx App Note "XAPP 029" beschrieben ist und 1 Bit pro Zyklus ausführt, wahrscheinlich mit 300 MHz +.

Wenn jemand eine gute Hybridtechnik kennt, wäre ich interessiert es zu wissen. Ich habe beide in Verilog mit Prüfständen in meiner verilog-utils -Sammlung modelliert.

Was Sie tun möchten, wird als Konvertierung in Binary Coded Decimal bezeichnet. Einige Computer verfügen über spezielle Anweisungen, die bei der Konvertierung von und zu BCD sowie bei der Addition und Subtraktion helfen. Dies ist jedoch für Sie nicht relevant.

Der einfachste Weg, Ihre 8-Bit-Zahl in zwei 4-Bit-Zahlen umzuwandeln, besteht darin, sie in Potenzen von 10 zu verarbeiten.

  vorzeichenloses Zeichen acht_bit_to_two_four_bit (vorzeichenloser Zeichenwert) {vorzeichenloses Zeichenergebnis = 0; Ergebnis = (Wert / 10) << 4; Ergebnis + = (Wert% 10); Ergebnis zurückgeben;}  

  vorzeichenloses Zeichen acht_bit_to_two_four_bit (vorzeichenloses Zeichenwert) {vorzeichenloses Zeichenergebnis = 0; Ergebnis = (Wert / 10) << 4; Ergebnis + = (Wert - Ergebnis * 10); Ergebnis zurückgeben;}  

Suchen Sie einen Binär-BCD-Konverter wie den 74185?

Wenn nicht, gibt es auf Wikipedia eine Liste der Logikchips der Serie 7400 Sie könnten durchsehen und finden, was Sie brauchen.

Eine Logikgatterlösung ist mithilfe einer Wahrheitstabelle und Karnaugh-Karten einfach. Die Wahrheitstabelle hat den Binärwert als Eingabe und den gewünschten BCD-Wert für die Ausgabe.

Ihre Wahrheitstabelle sollte folgendermaßen aussehen:

  a0 a1 a2 a3 | b6 b5 b4 b3 b2 b1 b0 <br>0 0 0 0 | 0 0 0 0 0 0 00 0 0 1 | 7-Seg-Ausgabe für 10 0 1 0 | 7-Seg-Ausgabe für 2 usw.  

Konvertieren Sie dann die Wahrheitstabelle in Karnaugh-Karten (K-Karten) und lösen Sie nach b6, b5 ... b0. Nehmen Sie die resultierenden Gleichungen und implementieren Sie sie mithilfe von Logikgattern.

Informationen zu K-Maps: http://en.wikipedia.org/wiki/Karnaugh_map

Und hier ist eine Lösung, die eine ähnliche Ausführung mit Nand-Gates durchläuft: http://circuitscan.homestead.com/files/digelec/bcdto7seg.htm

Bearbeiten: Aus dem Kommentare: Wenn Ihre 4-Bit-Zahl nicht unbedingt eine BCD darstellt, dh über 9 hinausgeht, würde ich die Gleichung direkt aus der Wahrheitstabelle ableiten. So zum Beispiel für diesen Eintrag in der Wahrheitstabelle:

  a0 a1 a2 a3 | output0 1 0 1 | 0 1 1 0 1 1 0  

Ihre Gleichung für das erste Bit (0) lautet a0 + a1 (Balken) + a2 + a3 (Balken), das zweite Bit (1) ist a0 ( bar) + a1 + a2 (bar) + a3 und so weiter. Das Implementieren dieser Gleichung in Logikgattern ist unkompliziert.

Bearbeiten2: Viele dieser Gleichungen überlappen sich und Sie können sie nach der Generierung weiter vereinfachen.

Wenn Sie die Schaltung so einfach wie möglich gestalten möchten, würde ich empfehlen, statt dezimal anzuzeigen, hexadezimal zu verwenden.In diesem Fall zeigt jede 7-Segment-Anzeige einen Wert von 0 bis 15 an, wobei die Zahlen 10, 11, 12, 13, 14 und 15 als A, B, C, D, E und F angezeigt werden. Dann benötigen Sie nur zwei MC14495-ICsum jeden 4-Bit-Wert in seine 7-Segment-Anzeigeausgänge umzuwandeln.