Die Antwort auf (1) lautet ja. Ich muss also nicht antworten (2).
Lassen Sie uns alles zufällig sortieren. Lassen Sie die Pfeile so laufen, wie Sie möchten. Wenden Sie dann das Kirchhoff-Spannungsgesetz und das Kirchhoff-Stromgesetz an.
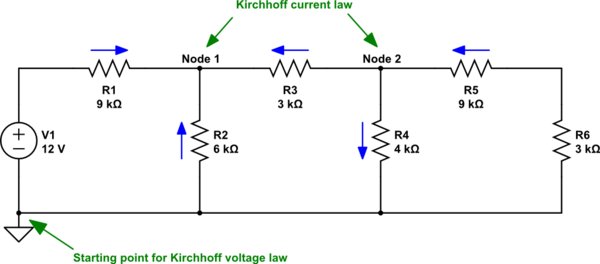
simulieren Sie diese Schaltung - Schema erstellt mit CircuitLab sup>
Ich habe Pfeile platziert, die anzeigen, was ich gerade gefühlt habe. War egal. Aber was auch immer ich mich entscheide, ich muss es natürlich konsequent verwenden, um die Gleichungen aufzustellen. Stellen wir also die Schleifengleichungen auf. Ich werde immer dort beginnen, wo sich der Boden in diesem Diagramm befindet. Der Schwanz eines Pfeils ist (+) und der Kopf ist (-). Wenn ich mich in einer Schleife bewege, verwende ich das Zeichen, auf das ich zum ersten Mal stoße, für das Zeichen des Begriffs. Also:
\ $ - 12 + 9k \ Omega \ cdot I_1 - 6k \ Omega \ cdot I_2 = 0 \ $
\ $ - 12 + 9k \ Omega \ cdot I_1 - 3k \ Omega \ cdot I_3 + 4k \ Omega \ cdot I_4 = 0 \ $
\ $ - 12 + 9k \ Omega \ cdot I_1 - 3k \ Omega \ cdot I_3 - \ left (9k \ Omega +) 3k \ Omega \ right) \ cdot I_5 = 0 \ $
Dann haben Sie auch diese aus Kirchhoffs aktuellem Gesetz. [Auch hier MÜSSEN Sie diese Pfeile beobachten, damit ein Pfeil, der in einen Knoten geht, (+) und ein Pfeil, der aus einem Knoten herausgeht, (-) ist]:
\ $ I_1 + I_2 + I_3 = 0 \ $
\ $ - I_3 - I_4 + I_5 = 0 \ $
Wenn Sie die obigen Gleichungen in einer Matrixgleichung anordnen, erhalten Sie:
\ $ \ left [beginnen \ {array} {} ccccc & 9000 -6000 & 0 & & 0 0 \\ 0 9000 & & -3000 & 4000 & 0 \\ 0 9000 & & -3000 & 0 & -12000 \\ 1 & 1 & 1 & 0 & 0 \\ 0 & 0 & -1 & -1 & 1 \ end {array} \ right]% \ left [\ begin {array} {c_ \ \\ I_5 \ end {array} \ right] = \ left [\ begin {array} {c} 12 \\ 12 \\ 12 \\ 0 \\ 0 \ end {array} \ right] \ $
Was sich wie folgt löst:
\ $ \ begin {array} {l} I_1 = 0,001 \\ I_2 = -0.0005 \\ I_3 = -0.0005 \\ I_4 = 0,000375 \\ I_5 = - 0,000125 \ end {array} \ $
Die Minuszeichen zeigen an, dass die gewählte Analyserichtung falsch war und geändert werden sollte. Ändern Sie also die Richtungspfeile für \ $ I_2 \ $, \ $ I_3 \ $ und \ $ I_5 \ $.
Es spielt also keine Rolle, was Sie zuerst denken. Wählen Sie einfach eine Richtung und bleiben Sie bei der Analyse dabei. Wenn Sie fertig sind, erfahren Sie in der Antwort, ob Sie es richtig ausgewählt haben oder nicht.
Mit anderen Worten: "Ja, mit Kirchhoffs Gesetzen können Sie die Anweisungen herausfinden."