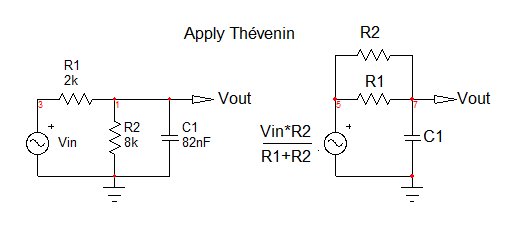
Wenn Sie sich mit einer Schaltung befassen, deren Übertragungsfunktion bestimmt werden muss, müssen Sie versuchen, die Komponenten und Quellen auf eine freundlichere Weise neu anzuordnen, damit die Dinge klarer werden. In Ihrer Schaltung sehen Sie beispielsweise, dass Sie einen Widerstandsteiler haben, der den Kondensator antreibt. Warum nicht hier Thévenin verwenden, um die Schaltungskomplexität zu reduzieren? Die Thévenin-Spannung vor dem Kondensator ist \ $ V_ {th} (s) = V_ {in} (s) \ frac {R_2} {R_1 + R_2} \ $ span> und der Thévenin-Widerstand ist \ $ R_ {th} = R_1 || R_2 \ $ span>. Wie in der folgenden Skizze gezeigt, haben Sie Ihre Schaltung auf einen einfachen Filter \ $ RC \ $ span> reduziert, dessen Übertragungsfunktion \ ist. $ \ frac {V_ {out} (s)} {V_ {th}} = \ frac {1} {1 + sC_1R_ {th}} \ $ span>. Wenn Sie jetzt \ $ V_ {th} (s) \ $ span> und \ $ R_ {th} (s) \ ersetzen $ span> Nach ihrer Definition und Neuanordnung sollten Sie \ $ H (s) = \ frac {V_ {out (s)}} {V_ {in} (s) finden. } = \ frac {R_2} {R_1 + R_2} \ frac {1} {1 + sC_1R_ {th}} \ $ span>.

Der Begriff \ $ C_1R_ {th} \ $ span> bildet die Schaltungszeitkonstante, deren Dimension die Zeit ist. Sie können diese Übertragungsfunktion in einem sogenannten Low-Entropy -Format wie \ $ H (s) = H_0 \ frac {1} {1+ umschreiben \ frac {s} {\ omega_p}} \ $ span> mit \ $ H_0 = \ frac {R_2} {R_1 + R_2} \ $ span> und \ $ \ omega_p = \ frac {1} {C_1 (R_1 || R_2)} \ $ span>. Dies ist der richtige Weg, um eine Übertragungsfunktion zu schreiben. Sie sehen, dass es einen Gleichstromgewinn gibt ( \ $ H_0 \ $ span>) und einen Pol, der durch \ $ \ omega_p \ $ gegeben ist span>.

Die andere einfachere Möglichkeit, die hier eingeführten schnellen Analysetechniken oder FACTs anzuwenden. Ihre Schaltung enthält ein Energiespeicherelement, den Kondensator, also eine Schaltung erster Ordnung. Der Stimulus ist Ihre Quelle \ $ V_ {in} \ $ span> auf der linken Seite, während die Antwort die Ausgabe ist signalisieren, dass ich \ $ V_ {out} \ $ span> aufgerufen habe. Die mathematische Beziehung, die die Antwort auf den Reiz verbindet, wird als Übertragungsfunktion bezeichnet. Es gibt viele Möglichkeiten, eine Übertragungsfunktion zu bestimmen. Ich habe festgestellt, dass der einfachste und intuitivste die FACTs verwendet. Durch einfache Manipulationen können Sie eine Übertragungsfunktion bestimmen, ohne eine einzelne Algebrazeile zu schreiben, indem Sie nur die Schaltung überprüfen.

Zuerst starten Sie in dc, \ $ s = 0 \ $ span>. In diesem Modus ist der Kondensator offen und Sie zeichnen Ihren Stromkreis neu, in dem die beiden Widerstände verbleiben. Die Übertragungsfunktion \ $ H \ $ span> verknüpft \ $ V_ {out} \ $ span> und \ $ V_ {in} \ $ span> notiert \ $ H_0 \ $ span> in diesem Modus ist

\ $ H_0 = \ frac {R_2} {R_1 + R_2} \ $ span>

Um die Zeitkonstante einer Schaltung zu bestimmen, haben Sie die Erregung auf 0 reduziert: Ihre linke Spannungsquelle \ $ V_ {in} \ $ span> ist reduziert auf 0 V. Ersetzen Sie es durch einen Kurzschluss. Entfernen Sie dann vorübergehend den Kondensator und bestimmen Sie in Ihrem Kopf den Widerstand, der in diesem Modus an den Anschlussklemmen "gesehen" wird. Siehe unten:

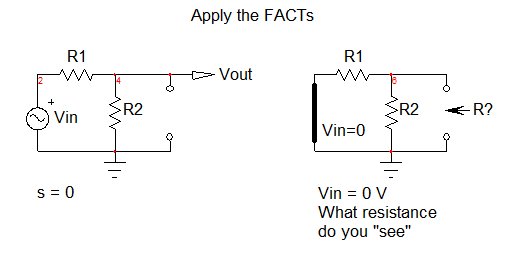
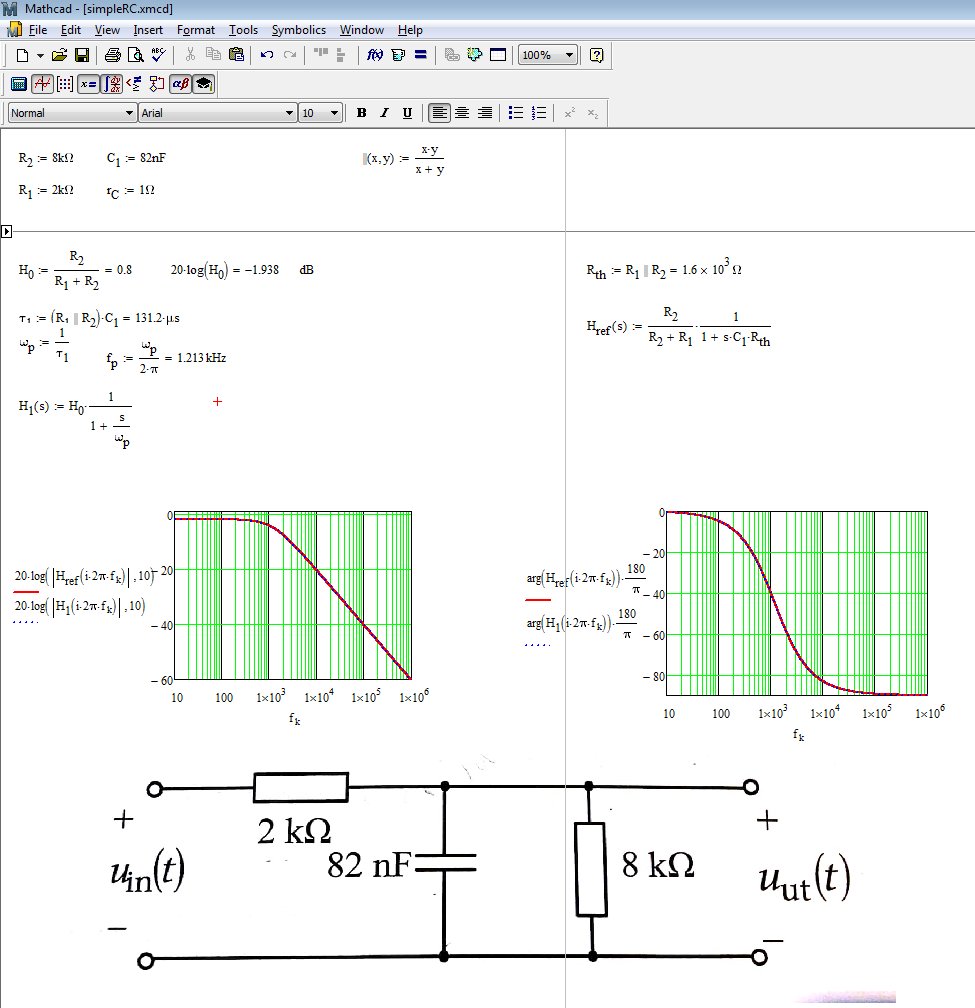
Sie sehen die parallele Kombination von \ $ R_1 \ $ span> und \ $ R_2 \ $ span>. Die Zeitkonstante ist also \ $ \ tau = C_1 (R_1 || R_2) \ $ span> und der Pol ist \ $ \ omega_p = \ frac {1} {\ tau} = \ frac {1} {C_1 (R_1 || R_2)} \ $ span>. Die Übertragungsfunktion wird sofort in der Form niedrige Entropie als \ $ H (s) = H_0 \ frac {1} {1+ \ frac {s bestimmt } {\ omega_p}} \ $ span> mit den von Ihnen festgelegten Werten. Mathcad kann Ihnen dabei helfen, diesen Ausdruck recht schnell zu zeichnen:

Und jetzt das i-Tüpfelchen, exklusiv für die FACTs. Was ist, wenn Sie einen kleinen Widerstand \ $ r_C \ $ span> in Reihe mit dem Kondensator \ $ C_1 \ $ span> hinzufügen? Nun, nur durch Inspektion, ohne eine Zeile Algebra zu schreiben, kann ich sehen, dass sich eine Null bei \ $ \ omega_z = \ frac {1} {r_CC_1} \ $ span befindet > und der neue Pol wird zu \ $ \ omega_p = \ frac {1} {C_1 (r_C + R_1 || R_2)} \ $ span>, die Gleichstromverstärkung bleibt gleich . Die aktualisierte Übertragungsfunktion in einem Formular mit niedriger Entropie wird zu \ $ H (s) = H_0 \ frac {1+ \ frac {s} {\ omega_z} } {1+ \ frac {s} {\ omega_p}} \ $ span>.

Ich ermutige Sie wirklich, die FACTs zu entdecken und zu beherrschen. Sie sind ein unglaubliches Analysewerkzeug, mit dem Sie Stunden algebraischer Kalkül sparen, die mit zunehmender Schaltungsreihenfolge häufig zu Lähmungen führen. Es gibt eine Einführung in die FACTs hier. Viel Spaß beim Lesen!

Entschuldigung, aber ich kann Ihrer Methode nicht folgen.

Da es sich um eine einpolige Übertragungsfunktion handelt, würde ich die einzelne Zeitkonstante \ $ \ tau = \ frac {1} {RC} \ $ bestimmen, wobei \ $ C = 82nF \ $ und \ $ R. \ $ ist der äquivalente Widerstand, den Ihr Kondensator "sieht". Dann berechnen Sie \ $ \ omega_1 \ $ als \ $ \ omega_1 = \ dfrac 1 \ tau \ $.

Der von der Kappe gesehene Widerstand ist der Widerstand parallel zur Kappe, wenn Sie die unabhängigen Spannungs- und Stromquellen im Stromkreis deaktivieren. In diesem Fall ist die einzige Quelle der Eingang, daher entspricht das Deaktivieren dem Kurzschluss der Eingangsanschlüsse (vorausgesetzt, es ist kein Quellenwiderstand zu berücksichtigen)

Deshalb haben Sie:

$$ R = R1 \ parallel R2 = 2k \ Omega \ parallel 8k \ Omega = 1,6k \ Omega $$

Daher:

$$ \ omega_1 = \ frac 1 {RC} = \ frac 1 {1.6k \ Omega \ times 82nF} \ ca. 7621 \ frac {rad} {s} $$

was einer Frequenz entspricht:

$$ f_1 = \ frac {\ omega_1} {2 \ pi} \ ca. 1213 Hz $$

Die A-Konstante erhalten Sie, wenn Ihre Frequenz auf Null abfällt, da es sich um eine Tiefpasskonfiguration handelt. Daher können Sie bei einer Frequenz von 0 die Kappe entfernen, da es sich um einen offenen Stromkreis handelt. Sie erhalten einen einfachen Spannungsteiler, dessen Verhältnis ist:

$$ A = \ frac {R2} {R1 + R2} = \ frac 8 {10} = 0,8 \ ca. -1,9 dB $$

Hier sind die Ergebnisse einer LTspice AC-Simulation Ihrer Schaltung:

Ein gezoomtes Bild der Grafiken mit aktivierten Cursorn bestätigt die obige Analyse:

Sie haben die Gesamtimpedanz von \ $ U_ {in} ^ + \ $ bis \ $ U_ {in} ^ - \ $ berechnet, das bringt uns nicht viel.Machen wir das richtig.

Ich hoffe, Sie können sehen, dass der Ausgang Teil eines Spannungsteilers ist.

$$ \ begin {align} U_ {ut} & = \ frac {82 nF // 8 kΩ} {2 kΩ + 82 nF // 8 kΩ} U_ {in} \\ \\ \ frac {U_ {ut}} {U_ {in}} & = \ frac {82 nF // 8 kΩ} {2 kΩ + 82 nF // 8 kΩ} \\ \\ \ frac {U_ {ut}} {U_ {in}} = H (\ omega) & = \ frac {\ frac {1} {j \ omega82 × 10 ^ {- 9}} // 8000} {2000+ \frac {1} {j \ omega82 × 10 ^ {- 9}} // 8000} \\ \ end {align} $$

Ich glaube, Sie können es von hier aus nehmen.

Mit dem TINA-Programm (www.tina.com) können Sie auch die Übertragungsfunktion und mehr automatisch generieren.Es ist auch großartig, Ihre manuell abgeleiteten Ergebnisse zu überprüfen.

Hier ist ein Video, wie es geht.Ich werde später die Lösung Ihres Beispiels hinzufügen https://www.youtube.com/watch?v=sf_cXw7pF9s&list=PLScrHAmLYSQCRUFsGcFVpRp0W3IvTy3Gt&index=15

Ich habe die Werte von Kondensator und Widerständen als Variablen beibehalten, was Ihnen im Allgemeinen das Leben beim Lösen erleichtert.