ThePhoton hat eine sehr gute Antwort gegeben. Im Folgenden finden Sie jedoch eine erweiterte Version mit vollständiger Ableitung der Formel und Einchecken in LTSpice sowie Leistungsübertragungsanalyse.
I. Die S-Matrix für das 2-Port-System lautet
$$ \ begin {pmatrix}
{\ frac {Z} {{2 {Z_0} + Z}}} & {\ frac {{2 {Z_0}}} {{2 {Z_0} + Z}}} \\
{\ frac {{2 {Z_0}}} {{2 {Z_0} + Z}}} & {\ frac {Z} {{2 {Z_0} + Z}}}
\ end {pmatrix}, $$
wobei \ $ Z \ äquiv. {1 \ über {j \ omega C}} \ $, \ $ {Z_0} \ $ die reale charakteristische Impedanz des Systems ist. Die Matrix gilt für jedes Z, sowohl mit resistiven als auch mit reaktiven Komponenten.
II. Derivation
Für echtes \ $ {Z_0} \ $
$$ {a_i} = {{{V_i} + {I_i} {Z_0}} \ über {2 \ sqrt {{Z_0}}}, \: {b_i} = {{{V_i} - {I_i} {Z_0 }} \ over {2 \ sqrt {{Z_0}}}} $$
Quelle: "Power Waves and the Scattering Matrix", K. Kurokawa, IEEE, 1965, URL.
Aus der Spannungsteilerregel
$$ {V_1} = {V_s} {{Z + {Z_0}} \ über {2 {Z_0} + Z}}, \: {V_2} = {V_s} {{{Z_0}} \ über {2 {Z_0 } + Z}} $$
Aus dem Ohmschen Gesetz
$$ {I_1} = {{{{V_s}} \ über {2 {Z_0} + Z}}} $$
Dann ist der Wert für den Eingangsreflexionskoeffizienten
$$ {S_ {11}} = {\ left. {{{{b_1}} \ over {{a_1}}} \ right | _ {{a_2} = 0}} = {{{V_1} - {I_1} {Z_0}} \ over {{V_1} + { I_1} {Z_0}}} = {{{V_s} {{Z + {Z_0}} \ über {2 {Z_0} + Z}} - {{{V_s}} \ über {2 {Z_0} + Z}} {Z_0}} \ über {{V_s} {{Z + {Z_0}} \ über {2 {Z_0} + Z}} + {{{V_s}} \ über {2 {Z_0} + Z}} {Z_0} }} = {Z \ over {2 {Z_0} + Z}} $$
Bei Anwendung von \ $ {I_2} = - {I_1} \ $ beträgt der Wert für die Vorwärtsverstärkung
$$ {S_ {21}} = {\ left. {{{{b_2}} \ über {{a_1}}} \ rechts | _ {{a_2} = 0}} = {{{V_2} - {I_2} {Z_0}} \ über {{V_1} + { I_1} {Z_0}}} = {{{V_2} + {I_1} {Z_0}} \ over {{V_1} + {I_1} {Z_0}}} = {{{V_s} {{{Z_0}} \ over {2 {Z_0} + Z}} + {{{V_s}} \ über {2 {Z_0} + Z}} {Z_0}} \ über {{V_s} {{Z + {Z_0}} \ über {2 { Z_0} + Z}} + {{{V_s}} \ über {2 {Z_0} + Z}} {Z_0}} = {{2 {Z_0}} \ über {2 {Z_0} + Z}} $$
Beachten Sie, dass \ $ {S_ {11}} + {S_ {21}} = 1 \ $, was erwartet wurde, wenn am zweiten Port keine eingehende Welle vorhanden war (\ $ {a_ {2}} = 0 \ $) .
III. Energieeinsparung
Was das Energieerhaltungsgesetz betrifft
$$ {\ left | {{a_1}} \ right | ^ 2} - {\ left | {{b_1}} \ right | ^ 2} = {\ left | {{b_2}} \ right | ^ 2} + \ Delta, $$
wo die \ $ {\ links | {{a_1}} \ right | ^ 2} - {\ left | {{b_1}} \ right | ^ 2} \ $ ist die vom Generator gelieferte Leistung, \ $ {\ left | {{b_2}} \ right | ^ 2} \ $ ist die von der Last verbrauchte Leistung, wobei das Delta die vom Prüfling verbrauchte Leistung ist.
Bitte beziehen Sie sich auf dasselbe Papier von Kurokawa, wenn nicht klar ist, warum diese speziellen Ausdrücke zur Berechnung der Energieübertragung verwendet werden.
Lassen Sie uns zeigen, dass im Fall eines Kondensators \ $ \ Delta \ $ Null ist (der Prüfling verbraucht keinen Strom). Erinnern an \ $ Z \ equiv {1 \ über {j \ omega C}} \ $
$$ {\ left | {{a_1}} \ right | ^ 2} - {\ left | {{b_1}} \ right | ^ 2} = {\ left | {{{{V_1} + {I_1} {Z_0}} \ über {2 \ sqrt {{Z_0}}}} \ right | ^ 2} - {\ left | {{{{V_1} - {I_1} {Z_0}} \ über {2 \ sqrt {{Z_0}}}} \ rechts | ^ 2} = {1 \ über {4 {Z_0}}} \ links ({ {{\ left | {{V_s} {{Z + {Z_0}} \ über {2 {Z_0} + Z}} + {{{V_s}} \ über {2 {Z_0} + Z}} {Z_0}} \ right |} ^ 2} - {{\ left | {{V_s} {{Z + {Z_0}} \ over {2 {Z_0} + Z}} - {{{V_s}} \ over {2 {Z_0} + Z}} {Z_0}} \ rechts |} ^ 2}} \ rechts) = {{{V_s} ^ 2} \ über {4 {Z_0}}} \ links ({{{\ links | {{{2 {Z_0} + Z} \ über {2 {Z_0} + Z}}} \ rechts |} ^ 2} - {{\ links | {{Z \ über {2 {Z_0} + Z}}} \ rechts |} ^ 2}} \ right) = {{{V_s} ^ 2} \ over {4 {Z_0}}} \ left ({1 - {{{{\ left | Z \ right |} ^ 2}} \ over { {{\ left | {2 {Z_0} + Z} \ right |} ^ 2}}} \ right) = {{{V_s} ^ 2} \ over {4 {Z_0}}} \ left ({1 - {{{1 \ über {{C ^ 2} {\ omega ^ 2}}} \ über {4Z_0 ^ 2 + {1 \ über {{C ^ 2} {\ omega ^ 2}}}} \ rechts) = {{{V_s} ^ 2} \ über {4 {Z_0}}} {{4Z_0 ^ 2} \ über {4Z_0 ^ 2 + {1 \ über {{C ^ 2} {\ omega ^ 2}} }}} = {V_s} ^ 2 {{{Z_0}} \ über {4Z_0 ^ 2 + {1 \ über {{C ^ 2} {\ omega ^ 2}}}} $$
Nun dasselbe für die übertragene Welle:
$$ {\ left | {{b_2}} \ right | ^ 2} = {\ left | {{{{V_2} - {I_2} {Z_0}} \ over {2 \ sqrt {{Z_0}}}} \ right | ^ 2} = {\ left | {{{{V_2} + {I_1} {Z_0}} \ über {2 \ sqrt {{Z_0}}}} \ rechts | ^ 2} = {1 \ über {4 {Z_0}}} \ links ({ {{\ left | {{V_s} {{{Z_0}} \ over {2 {Z_0} + Z}} + {{{V_s}} \ over {2 {Z_0} + Z}} {Z_0}} \ right |} ^ 2}} \ right) = {{{V_s} ^ 2} \ over {4 {Z_0}}} {\ left | {{{2 {Z_0}} \ über {2 {Z_0} + Z}}} \ rechts | ^ 2} = {{{V_s} ^ 2} \ über {4 {Z_0}}} {{4Z_0 ^ 2} \ over {4Z_0 ^ 2 + {1 \ over {{C ^ 2} {\ omega ^ 2}}}} = {V_s} ^ 2 {{{Z_0}} \ over {4Z_0 ^ 2 + {1 \ over {{C ^ 2} {\ omega ^ 2}}}} = {\ left | {{a_1}} \ right | ^ 2} - {\ left | {{b_1}} \ right | ^ 2}, \, \ Rightarrow \ Delta = 0. $$
IV. Extraktion von s-Parametern in LTSpice und Überprüfung der analytischen Formel
Lassen Sie uns abschließend einen s-Parameter mit LTSpice extrahieren und mit unserer analytischen Formel vergleichen. Machen wir es zum Beispiel für \ $ {S_ {21}} \ $:
$$ \ left | {{S_ {21}}} \ right | = \ left | {{{2 {Z_0}} \ over {2 {Z_0} + Z}}} \ right | = {{2 {Z_0}} \ over {\ sqrt {4Z_0 ^ 2 + {1 \ over {{C ^ 2} {\ omega ^ 2}}}} = 0,30, \, $$
bei \ $ {Z_ {0}} \ $ = 50 Ohm, \ $ \ omega \ $ = 10 MHz und C = 50 pF.
Extraktion in LTSpice:
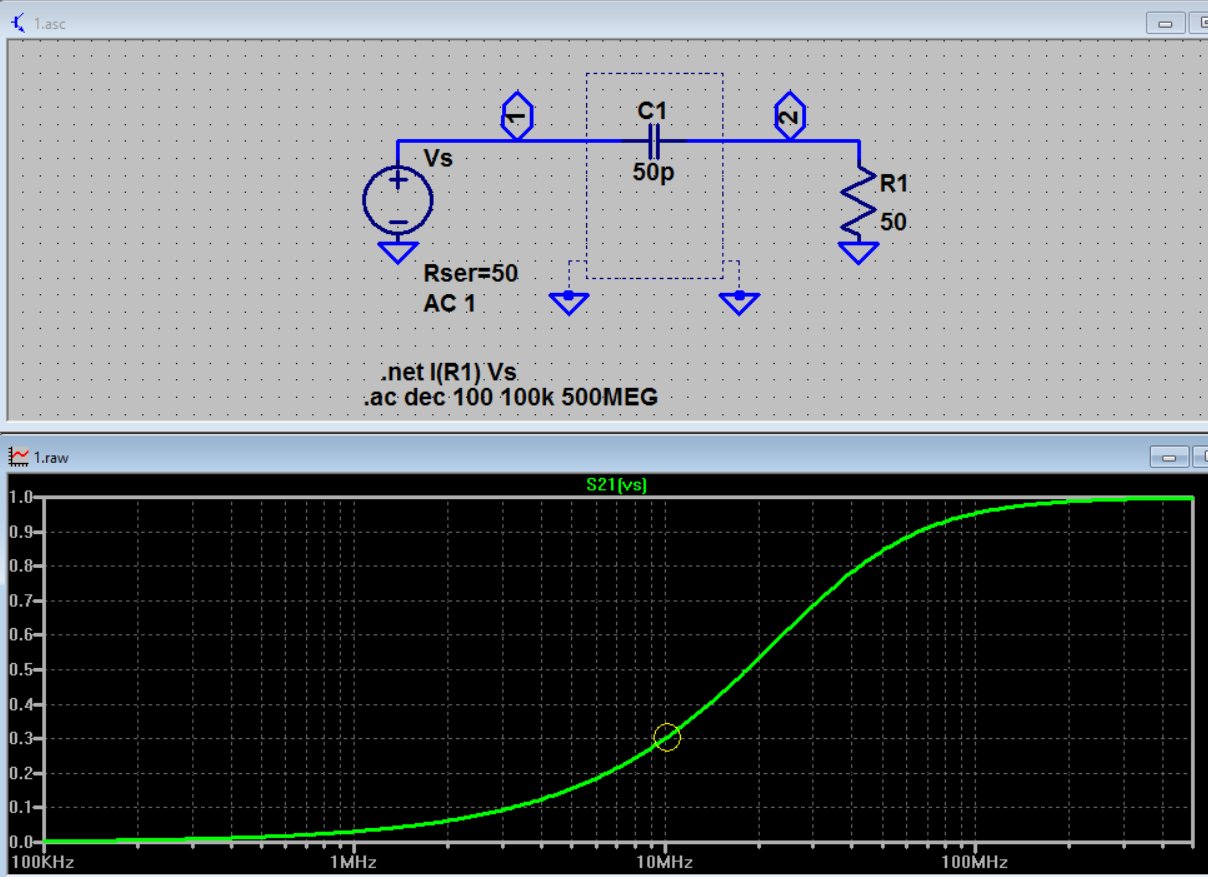
In dieser Tabelle steht, dass
1) Bei niedrigeren Frequenzen ist die Vorwärtsverstärkung gering (nichts bricht zur Last durch), da sich der Kondensator wie offen verhält.
2) Bei höheren Frequenzen liegt die Vorwärtsverstärkung nahe bei eins: Die eingehende Leistungswelle wird vollständig an die Last übertragen, da sich der Kondensator so kurz verhält.