Obwohl diese Frage beantwortet wurde, wollte ich nur etwas für diejenigen hinzufügen, die ein ideales logarithmisches Potentiometergesetz für die Simulation suchen. Eine Abbildung vom linearen Gesetz zum logarithmischen Gesetz kann in der allgemeinen Form gefunden werden:

$$ y = a \ b ^ {x} + c $$

Lassen Sie diese Gleichungsfunktion eine Zuordnung von \ $ 0 \ leq x \ leq1 \ $ zu \ $ 0 \ leq y \ leq 1 \ $ definieren, wobei \ $ a \ $, \ $ b \ $ und \ $ c \ $ sind freie Parameter, die an die gewünschten Kurven angepasst werden können.

Dies ist eine Gleichung mit drei freien Parametern, sodass wir drei Einschränkungen auswählen können, um die Parameterwerte abzuleiten. Für ein ideales Potentiometer sollte der Ausgang keinen Widerstand haben, wenn der Wischer ganz auf das Minimum eingestellt ist. Daher ist \ $ y = 0 \ $, wenn \ $ x = 0 \ $ und so weiter $$ 0 = a + c, \ quad c = -a $$ Jetzt haben wir also die Gleichung: $$ y = ab ^ x - a. $$ Unser zweites Ziel ist es, maximalen Widerstand zu haben, wenn der Scheibenwischer bis zum Maximum reicht, d. H. \ $ Y = 1 \ $, wenn \ $ x = 1 \ $ $$ 1 = ab - a = a (b-1), \ quad a = \ frac {1} {b-1}. $$

Schließlich können wir einen Mittelpunkt auswählen, den die Kurve durchlaufen soll, den ich als benutzerdefinierbar als \ $ y = y_m \ $ belassen werde, wenn \ $ x = 0,5 \ $. Das gibt uns $$ y_m = a (\ sqrt {b} - 1) = \ frac {\ sqrt {b} - 1} {b - 1} = \ frac {1} {\ sqrt {b} +1} $$ und schlussendlich $$ b = \ left (\ frac {1} {y_m} - 1 \ right) ^ 2 $$

Dies gibt uns ein parametrisches logarithmisches Potentiometergesetz, das den Kurvenbetrag ändern kann. Denken Sie daran, dass bei \ $ y_m = 0.5 \ $ \ $ a = \ infty \ $. Sie könnten eine lineare Karte erstellen, wenn Sie \ $ y_m = 0.5 - 10 ^ {- 5} \ $ oder etwas anderes wählen (aber warum sollten Sie!).

Normalerweise sind Audio-Taper-Potis nicht logarithmisch, sondern eine stückweise Annäherung mit nur 2 Segmenten.

Jedes Segment der Spur wird mit einem Material mit unterschiedlichem spezifischen Widerstand beschichtet oder hat eine andere Breite als die anderen Segmente.

Ich habe drahtgewickelte Verjüngungstöpfe gesehen, bei denen die erstere eine sich allmählich ändernde Breite aufweist, um die unterschiedliche Neigung zu erreichen.

Ein linearer Topf kann möglicherweise als logarithmischer Konus verwendet werden, indem ein Widerstand zwischen den Scheibenwischer und einen Anschluss gelegt wird, wie im zweiten Diagramm gezeigt ( Vom Elliot Sound Products-Handbuch zu Potentiometern.)

Es gibt keine Formel für einen Log Pot. Das Beste, was Sie erwarten können, ist, dass die Änderung des Widerstands pro Winkel am "unteren" Ende viel geringer ist als die am "oberen" Ende. Es wäre schön, wenn es logarithmisch wäre, aber es ist nicht.

Eine Antwort von Kevin weist darauf hin, dass die häufigste Annäherung darin besteht, dass die Spur zwei verschiedene lineare (ish) Abschnitte aufweist. Dies ist billiger herzustellen als eine sich ständig ändernde Verjüngung und billiger als 3 oder mehr Abschnitte.

Leider hat der Ausdruck "Log Taper" mehr Freiheitsgrade als nur den Gesamtwiderstand. Das Empfindlichkeitsverhältnis von oben nach unten wird ebenfalls benötigt. Wenn ich also einen echten Log-Topf kaufe, muss ich einen Topf mit 2 Oktaven oder einen Topf mit 3 Oktaven angeben. Die Hersteller und Händler müssten mehrere Typen führen, von denen jeweils weniger verkauft werden, was viel mehr kostet. Für eine Audioanwendung möchten Sie wahrscheinlich sowieso kein echtes Protokoll, sondern möchten sich auf einer niedrigen Ebene vom Protokoll lösen und linear auf Null sinken.

Der Grund warum es keine definierte logarithmische Verjüngung gibt, ist, dass sich kein Kundenstamm genug darum kümmert, was die Verjüngung genau zu zahlen bereit ist, damit die Hersteller sich die Mühe machen, etwas zu standardisieren. Log-Töpfe werden hauptsächlich in Audiogeräten verwendet. Solange das Rotationsgesetz einigermaßen zahm ist, kümmert sich kein Kunde wirklich darum, dass der Topf (sagen wir) 20 dB pro 90 Grad liefert. Er möchte lediglich einen Pegel einstellen.

Interessanterweise war die BBC bereits in den 50er / 60er Jahren im IIRC mit diesem Problem konfrontiert, als sie neue Studioausrüstungen entwerfen wollte, und stellte fest, dass sie keine gleichen Log-Töpfe aus verschiedenen Quellen erhalten konnten. Also erfanden sie eine saubere Schaltung, die einen linearen Topf verwendete, um die logarithmische Leistung zu erhalten, aber da es sich um einen linearen Topf handelte, war er immer reproduzierbar. Sehen Sie, ob Sie einfach beschreiben können, wie es funktioniert und warum es nicht knistert.

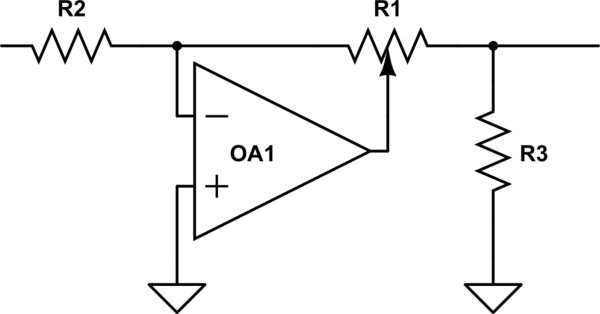
^{simulieren diese Schaltung - Schema erstellt mit CircuitLab sup>}

Wenn Sie ein Experiment einrichten, um die Protokollgesetze Ihres Topfes zu messen, erwarten Sie, dass das Gesetz eines anderen Herstellers unterschiedlich ist.

Dieses von der BBC verwendete Schema hat mir sehr gut geholfen, einen Log-Pot aus einem einfachen Lin-Pot in meinen Arduino-Projekten zu erstellen.Ich habe nachgerechnet.Hier die Ergebnisse:

Sei 'a' die Einstellung des Potentiometers (von 0 bis 1).'H' ist die Übertragungsfunktion (natürlich in Software implementiert).

H = a / (1 + (1 - a) * K)

Mit K = 2 liefert dies eine wirklich schöne Annäherung an eine Log-Funktion mit einem Wert von 0,25 bei 'a' = 0,5.

Für 0,1 (eigentlich 0,125) als Halbwertswert funktioniert Folgendes gut:

H = a * a / (1 + (1 - a) * K);mit K = 2

Ich habe ein digitales Potentiometer verwendet, um als grobe Lautstärkeregelung zu fungieren.Das eingehende Signal geht an ein Ende des Topfes, das ausgehende Signal kommt vom Scheibenwischer und die gemeinsame Masse befindet sich am anderen Ende.Also wenn

M = Gesamtwiderstand des Potentiometers

R = Widerstand zwischen "Nullvolumen" und Wischer

A = erforderliche Dämpfung in dB

Dann scheint das ganz gut zu funktionieren:

$$ R = M \ 10 ^ {(A / 10)} $$ span>

Wie andere bereits erwähnt haben, beträgt das "Null" -Ende des Topfwegs -∞ dB. Sie müssen also irgendwann auf die lineare Reduzierung von Dezibel verzichten.Oberhalb dieses Grenzwerts möchten Sie möglicherweise, dass äquivalente Pot-Turns äquivalenten Dezibeländerungen entsprechen - möglicherweise 5 Grad CCW-Schnitte von 1 dB.